判定差のお話2
2019.06.01
前回のつづき
・ボタンのポーリングはVSYNCに同期する(GPUクロック基準)。ちなみに処理落ち時はポーリングしないらしい。
・判定処理はVSYNCに同期して行われるが、判定基準はフレーム数ではなくタイマー(厳密には全然違うがイメージとしてはミリ秒単位の現在時刻)基準で判定する。
というわりとギルティな仕組みが見えてきました。
まあこれだけでは説明できない現象もあるんだけども、少なくとも筐体1と筐体2で判定差が発生する可能性は大いにあり得る話です。
ところで実際、この、「製造個体差」ってのがどのくらいあるのか、っていう話になるんだけども、手元のNu基板2台を実測した結果、
基板1:VSYNC=60.0014Hz
基板2:VSYNC=60.0023Hz
と、なってました。ちなみにきちんと校正されてる測定器ではないので、実際の値としてどのくらい信憑性があるかというのはありますが、相対的にどのくらい変わっているか、という指標にはなるとおもいます。
ちなみに、HDMIを測定するような測定器は持っていないので、DVI-IのアナログVSYNC出力の測定値です。
基板1が60Hzに対して+23ppm
基板2が60Hzに対して+38ppm
で、差は15ppmです。これがワーストケースなのかは解りませんが、実際のところこのくらい変動はするようです。
15ppmなので、以前に書いた水晶振動子の製造誤差±30ppmからみても妥当な範囲かと思われます。
さて、ではここまでの流れの整理です。
・定数値の整理
判定の基準となる時間に関する定数です。2進浮動小数点なので10進の小数表記にした場合、かならず丸め誤差が発生します。
フレーム数換算としたとき、誤差がどのくらい出るのかを確認します。
0.03 ≒ 1.8/60-(9/13421772800)
0.07 ≒ 4.2/60+(1/ 3355443200)
0.10 ≒ 6.0/60+(1/ 671088640)
0.13 ≒ 7.8/60-(1/ 209715200)
0.167≒10.0/60+(1/ 201326592)
0.017≒ 1.0/60+(7/ 8053063680)
誤差(式の右側に分母がやたら大きい分数で書かれている部分)で、一番大きい値は、
(1/201326592)
です。
DIVAをする上で、1曲あたり240秒として、この誤差が積算したとしても、
(1/201326592)×240=5/4194304秒
フレーム数に換算しても、×60で、
75/1048576=0.00007フレームなので、まあ1曲でこの程度の誤差なら無視できるでしょう。たぶん。
なので、定数値はすべて上記に記載のフレーム数として考えます。
・想定される動作
基本的に焼き直しな内容ですが、より具体的に書いてみます。
まず、曲開始時に、VSYNCとタイマーとポーリングは一旦同期するとします。
※一番最初にVSYNCに同期してタイマーを取得して、そこからの差分時間で判定する前提(未確認、この前提の確証を取らないと…)。
ここでは計算しやすくするためにbpm=120とし、四分音符ノーツとします。
四分音符ノーツは必ず開始から0.5秒単位のところがジャストタイミングになりますね。
なので、VSYNCとタイマーが正確に同期していれば、必ず30フレーム単位で現れることになります。
bpm120なので、10拍でMAX BOUNSになります。厳密に言うと10拍+1fpsでMAX BONUSです。
HOLD開始の10拍後に押し直しノーツがあった場合、図のタイミングだと早Cで入ってMAXを取った後、遅Cを取れる計算になります。
本来であれば、bpm=120なので、VSYNCタイミングとジャストタイミングの位置関係は崩れません(図※A箇所)。

※クリックで拡大
ここで、VSYNCが若干遅い、もしくはタイマーが若干速いという誤差を持った状態を考えてみます。
そうすると、VSYNCからジャストタイミングまでの時間が徐々に短くなっていきます。
図にすると下記です。

※クリックで拡大
C-C MAXがどう頑張っても入らなくなりましたね。
これが現時点で考えられる、判定差の要因です。
さて、この現象が起きる原因は「GPUクロック」と「タイマー」の誤差の大きさによります。
単純に大きければ大きいほどおきやすいのではなく、誤差が特定の範囲の場合、特定のノーツに影響を及ぼす、となります。
なので、理論上「曲AのC-Cが入りやすい筐体は、曲BのC-Cも入りやすい。でも、曲CのC-Cは逆に入らない。そして曲CのC-Cが入る筐体は、曲DのC-Cも入れやすい」という現象になると思われます。
さてここで先日紹介したガチ勢による検証動画ですが、
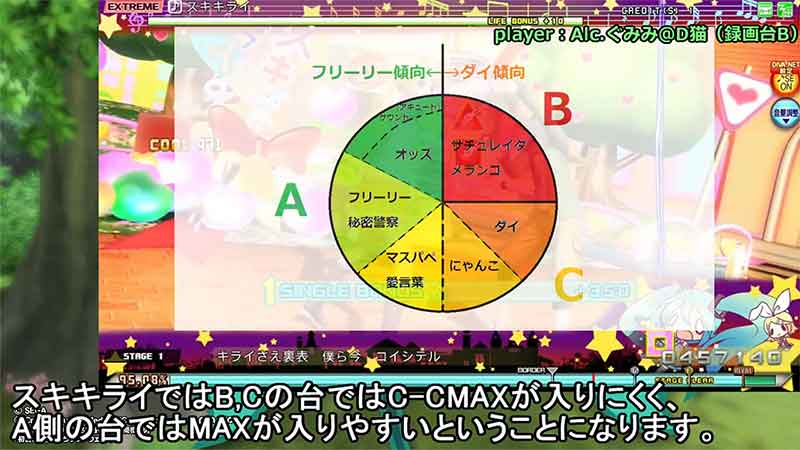
どうやら本当にそういう分類別けがされるようです。何傾向か、というのが恐らく誤差量によって決まってくるのかと思います。
コード解析からたどり着く理論上の予想と、ガチ勢プレイヤーの体感(?)による結果が同じって凄いと思うよ・・・。
そして、この原因となるVSYNCタイミング(≒ポーリング/判定タイミング)とタイマーの誤差を体感ではなく明確にどうやって(デバッガーとかを使わないで)実機で確認をすることができるか、という事になりますが、
・描画はVSYNCに同期して行われるが、針の角度・飛んでくるノーツの位置はタイマーを基準に計算される
→「今のVSYNCタイミング」から、「ジャストタイミング」までの時間(フレーム数ではなくタイマー基準)を元に描画
というところだと思います。なので、判定が異なる条件では、針の角度・飛んでくるノーツの位置が異なるはずです。
というのもまた、どうやら既出の情報のようです。
ところで、最初に規定した、「曲開始時に、VSYNCとタイマーとポーリングは一旦同期する」について、
もしこの前提が崩れた場合に何が起こるかというと、
毎回VSYNCとポーリングの位置関係が崩れる、ということです。
ちなみに、位置関係が崩れて始まったとしても、プレイ中にずれていく位置関係の速度は変わりません。
なので「この台はC-Cが入るときもあるが入らないときもある」となります。
仮に最初に同期しなかったからといって、この現象が発生しないわけではなく、筐体差として判別しにくくなる、というだけですね。
とまあ、判定差の原因の一つについてわりと掘り下げれた感じはありますが、これでも説明が付かない挙動はあります。
ステージ差・PV分岐差がまったく原因不明です。
起動差についても、仮にプレイ開始時のタイミング同期処理があった場合は発生しないはずです。
うん、まったく原因不明なのは解析のしようが無い。
次はとりあえずプレイ開始時のタイミング同期処理の確証を探そうかな。
・ボタンのポーリングはVSYNCに同期する(GPUクロック基準)。ちなみに処理落ち時はポーリングしないらしい。
・判定処理はVSYNCに同期して行われるが、判定基準はフレーム数ではなくタイマー(厳密には全然違うがイメージとしてはミリ秒単位の現在時刻)基準で判定する。
というわりとギルティな仕組みが見えてきました。
まあこれだけでは説明できない現象もあるんだけども、少なくとも筐体1と筐体2で判定差が発生する可能性は大いにあり得る話です。
ところで実際、この、「製造個体差」ってのがどのくらいあるのか、っていう話になるんだけども、手元のNu基板2台を実測した結果、
基板1:VSYNC=60.0014Hz
基板2:VSYNC=60.0023Hz
と、なってました。ちなみにきちんと校正されてる測定器ではないので、実際の値としてどのくらい信憑性があるかというのはありますが、相対的にどのくらい変わっているか、という指標にはなるとおもいます。
ちなみに、HDMIを測定するような測定器は持っていないので、DVI-IのアナログVSYNC出力の測定値です。
基板1が60Hzに対して+23ppm
基板2が60Hzに対して+38ppm
で、差は15ppmです。これがワーストケースなのかは解りませんが、実際のところこのくらい変動はするようです。
15ppmなので、以前に書いた水晶振動子の製造誤差±30ppmからみても妥当な範囲かと思われます。
さて、ではここまでの流れの整理です。
・定数値の整理
判定の基準となる時間に関する定数です。2進浮動小数点なので10進の小数表記にした場合、かならず丸め誤差が発生します。
フレーム数換算としたとき、誤差がどのくらい出るのかを確認します。
0.03 ≒ 1.8/60-(9/13421772800)
0.07 ≒ 4.2/60+(1/ 3355443200)
0.10 ≒ 6.0/60+(1/ 671088640)
0.13 ≒ 7.8/60-(1/ 209715200)
0.167≒10.0/60+(1/ 201326592)
0.017≒ 1.0/60+(7/ 8053063680)
誤差(式の右側に分母がやたら大きい分数で書かれている部分)で、一番大きい値は、
(1/201326592)
です。
DIVAをする上で、1曲あたり240秒として、この誤差が積算したとしても、
(1/201326592)×240=5/4194304秒
フレーム数に換算しても、×60で、
75/1048576=0.00007フレームなので、まあ1曲でこの程度の誤差なら無視できるでしょう。たぶん。
なので、定数値はすべて上記に記載のフレーム数として考えます。
・想定される動作
基本的に焼き直しな内容ですが、より具体的に書いてみます。
まず、曲開始時に、VSYNCとタイマーとポーリングは一旦同期するとします。
※一番最初にVSYNCに同期してタイマーを取得して、そこからの差分時間で判定する前提(未確認、この前提の確証を取らないと…)。
ここでは計算しやすくするためにbpm=120とし、四分音符ノーツとします。
四分音符ノーツは必ず開始から0.5秒単位のところがジャストタイミングになりますね。
なので、VSYNCとタイマーが正確に同期していれば、必ず30フレーム単位で現れることになります。
bpm120なので、10拍でMAX BOUNSになります。厳密に言うと10拍+1fpsでMAX BONUSです。
HOLD開始の10拍後に押し直しノーツがあった場合、図のタイミングだと早Cで入ってMAXを取った後、遅Cを取れる計算になります。
本来であれば、bpm=120なので、VSYNCタイミングとジャストタイミングの位置関係は崩れません(図※A箇所)。

※クリックで拡大
ここで、VSYNCが若干遅い、もしくはタイマーが若干速いという誤差を持った状態を考えてみます。
そうすると、VSYNCからジャストタイミングまでの時間が徐々に短くなっていきます。
図にすると下記です。

※クリックで拡大
C-C MAXがどう頑張っても入らなくなりましたね。
これが現時点で考えられる、判定差の要因です。
さて、この現象が起きる原因は「GPUクロック」と「タイマー」の誤差の大きさによります。
単純に大きければ大きいほどおきやすいのではなく、誤差が特定の範囲の場合、特定のノーツに影響を及ぼす、となります。
なので、理論上「曲AのC-Cが入りやすい筐体は、曲BのC-Cも入りやすい。でも、曲CのC-Cは逆に入らない。そして曲CのC-Cが入る筐体は、曲DのC-Cも入れやすい」という現象になると思われます。
さてここで先日紹介したガチ勢による検証動画ですが、

どうやら本当にそういう分類別けがされるようです。何傾向か、というのが恐らく誤差量によって決まってくるのかと思います。
コード解析からたどり着く理論上の予想と、ガチ勢プレイヤーの体感(?)による結果が同じって凄いと思うよ・・・。
そして、この原因となるVSYNCタイミング(≒ポーリング/判定タイミング)とタイマーの誤差を体感ではなく明確にどうやって(デバッガーとかを使わないで)実機で確認をすることができるか、という事になりますが、
・描画はVSYNCに同期して行われるが、針の角度・飛んでくるノーツの位置はタイマーを基準に計算される
→「今のVSYNCタイミング」から、「ジャストタイミング」までの時間(フレーム数ではなくタイマー基準)を元に描画
というところだと思います。なので、判定が異なる条件では、針の角度・飛んでくるノーツの位置が異なるはずです。
というのもまた、どうやら既出の情報のようです。
この微細なズレお分かりいただけるだろうか。見る場所見れば確かに違うけど、サラッと見ただけじゃ絶対気づけない。 pic.twitter.com/88QDcGaJXj
— ねあ (@nea0808) July 12, 2016
ところで、最初に規定した、「曲開始時に、VSYNCとタイマーとポーリングは一旦同期する」について、
もしこの前提が崩れた場合に何が起こるかというと、
毎回VSYNCとポーリングの位置関係が崩れる、ということです。
ちなみに、位置関係が崩れて始まったとしても、プレイ中にずれていく位置関係の速度は変わりません。
なので「この台はC-Cが入るときもあるが入らないときもある」となります。
仮に最初に同期しなかったからといって、この現象が発生しないわけではなく、筐体差として判別しにくくなる、というだけですね。
とまあ、判定差の原因の一つについてわりと掘り下げれた感じはありますが、これでも説明が付かない挙動はあります。
ステージ差・PV分岐差がまったく原因不明です。
起動差についても、仮にプレイ開始時のタイミング同期処理があった場合は発生しないはずです。
うん、まったく原因不明なのは解析のしようが無い。
次はとりあえずプレイ開始時のタイミング同期処理の確証を探そうかな。
判定差のお話
2019.04.28
前回の続きっぽい別バナです。
って感じに前後関係が追いにくいからblogって嫌いなのよね。このあたりはそのうちまとめて別ページにします。
まず判定差(ここではプレイの度に挙動が違う場合のある動作すべての意味)について、ガチ勢な方から提供頂いた貴重な情報をまとめてみます。
Ringedge時代はさらに他にも要因があったようですがとりあえずそこは省略します。
・筐体差
筐体(Nu/IOボード)に依存する固有の挙動。基本的に固定。アップデートで変化することがある。
・日付差/起動差
divaアプリ自体の再起動(筐体再起動/一旦Nuのサービスモードに戻る等)をする度に判定が変化することがある。
・ステージ差
特定のステージのみで判定が変化することがある。
・PV分岐差
分岐する/しないにより、その後のノーツの判定が変化することがある。
・時間差
上記の要因によらず、判定が変化することがある。
ということらしいですが、もちろん体感さっぱりわからん。
判別方法というのもあるらしく、
とのことだけど
「○が広ければxxx台」
とか言われてもどうやって○が広いかどうかを判別しろと。いや、原理は解るけどできません。
ところで、ここの記事はあくまで判定差の原因を突き止めようというだけで、ハイスコアを出してランキングインを目指そう、とかそういうページではないですよ。
腕があればお立ち台とか載ってみたいがな!
というわけなので、情報ソースはランカーの人達が気にするノーツ、つまりHOLDの入出ノーツになるけど、そんなに偶然キーとなるノーツばかりが変化する訳はないので、スコアタに関係ないノーツでもこのような事象は発生しているはず。
ただ、何をもって、「変化した」と定義するかは難しい。
たとえば「C-C MAX」が限られた条件だけで入るという判定差で、もしその筐体のすべての動作が正確に2倍速で動いたとして、超人が居ればやはり「C-C MAX」は入る。明らかに実時間で言えばCOOL期間は半分だけど、それは今回の検証として「変化した」とは言えない。
やはり、指標としては、ホールドノーツのちょうど5秒後にノーツがあって、MAXを取った後に判定がどうなるか、かな。
前回の解析結果によると、SAD/SAFEが一番期間が短いので、SAFEでホールド入って、5秒後のノーツでMAX取ったあとにSAFEを取れるか、とか。
でもHOLDを絡めないで検証したいんだよね。
※HOLDを絡めると、PVをそこまで進めないと検証できない、という、めんどくさいだけの話です。
まあそれはそれとして、課題だった奴。HOLD点の増加基準。結果解れば単純ですが、処理は結構やっかいでした。
はい、またいきなりソースです。HOLD関連処理関数です。
・引数
rcx=HOLD処理構造体アドレス
r8=押されているボタン(0x40)、○(0x80)、×(0x100)、□(0x200)のor
xmm1=前回この関数が呼ばれてからの経過時間
ちなみにこの関数自体は、どうやらVSYNCに同期して呼び出されるようです。
わりと冗長な処理とかもあるので関係ないところはがっつり削ったり順序変えたりしてます
14012C9F3: mov rdi,rcx
14012C9F6: mov ecx,dword ptr [rcx+0Ch] ;ホールド状態
14012CA15: dec ecx
14012CA17: je 000000014012CA97 ;ホールド中はjmp
14012CA1C: dec ecx
14012CA1E: je 000000014012CA73 ;MAX到達で飛ぶ
14012CA97: mov ecx,dword ptr [rdi+10h] ;ホールド中のボタン。
14012CA9A: test ecx,ecx
14012CA9C: je 000000014012CA44
14012CA9E: mov eax,ecx
14012CAA0: and eax,r8d
14012CAA3: cmp eax,ecx
14012CAA5: jne 000000014012CA84 ;押されているボタンが減った処理へ
14012CAAC: xorps xmm0,xmm0
14012CAA7: addss xmm6,dword ptr [rdi+14h] ;ホールド開始からの時間
14012CAB8: movss dword ptr [rdi+14h],xmm6 ;ホールド時間を更新
14012CAB4: mov r15d,dword ptr [rdi+18h] ;ホールド点(ゲーム中のHOLDボーナスバー表示)
14012CABD: subss xmm6,dword ptr [rdi+2Ch] ;最後にボタンが追加されてからの時間
14012CACC: comiss xmm6,dword ptr [140999A70h] ;5.000
14012CAD3: jb 000000014012CADD ;最後にボタン追加されてから5秒経ってないとjmp
14012CAD5: movss xmm6,dword ptr [140999A70h] ;5.000を超過したら5.000に丸め込み
14012CADD: comiss xmm6,dword ptr [rdi+1Ch] ;0.167。ただしボタン追加されたら0になる。
14012CAE1: jbe 000000014012CB2D ;ホールド開始から0.167s経過していないとjmp
14012CAE3: mov r8d,dword ptr [rdi+24h] ;1フレームあたりのホールド点。ボタン数で変化
14012CAE7: mov eax,r8d
14012CAEA: cdq
14012CAEB: sub eax,edx
14012CAED: sar eax,1
14012CAEF: movd xmm0,r8d
14012CAF4: cvtdq2ps xmm0,xmm0
14012CAF7: mulss xmm0,xmm6
14012CAFB: divss xmm0,dword ptr [rdi+20h] ;[rdi+20h]=常に0.017 xmm0=xmm0/0.017
14012CB00: cvttss2si ecx,xmm0
14012CB04: add eax,ecx
14012CB06: cdq
14012CB07: idiv eax,r8d
14012CB0A: mov ebx,eax
14012CB0C: imul ebx,r8d ;ebx=round([rdi+24h] * xmm6 / [rdi+20h])
14012CB10: cmp dword ptr [rdi],esi
14012CB12: jne 000000014012CB23
14012CB2D: mov ecx,dword ptr [rdi+30h] ;ホールド追加した時点の点数
14012CB30: add ecx,ebx
14012CB36: mov ebp,ecx
14012CB38: mov dword ptr [rdi+18h],ecx
;ebp=現時点の総ホールド点
;r15d=加算済みホールド点
14012CB41: sub ebp,r15d ;今回の加算点
14012CB52: comiss xmm6,dword ptr [140999A70h] ;5.000
14012CB59: mov dword ptr [rax+74h],3
14012CB60: mov dword ptr [rax+78h],ebx
14012CB63: mov dword ptr [rax+7Ch],r12d
14012CB67: jb 000000014012CA4C ;5.000未満
;MAX到達処理
14012CB6D: mov eax,dword ptr [rdi+34h] ;同時押しボタン数
14012CB7B: imul eax,eax,5DCh ;eax*1500=MAXボーナス
14012CB81: mov dword ptr [rdi+3Ch],eax ;MAX点を保持、この時点では加算されない
14012CB74: mov dword ptr [rdi+0Ch],2
14012CB84: jmp 000000014012CA4C
;ホールドMAXでここにくる
14012CA79: mov ebp,dword ptr [rdi+3Ch]
14012CA95: jmp 000000014012CA4C
14012CA4C:
14012CA60: mov eax,ebp ;戻り値代入
14012CA72: ret
つまりどういうことかというと、
・ホールドは開始から0.167秒は加算されない(知らなかった・・・)
・得点(MAX BONUS除く)はround(基準点(10~40) × ホールド秒 ÷ 0.017)
・ホールドMAX BONUSは、ホールドMAXの次のフレームで加算
ですね。
ところで、単精度浮動小数点の丸め込み誤差っていうのに気づいて、上記0.017とかは正確ではありません。
0.167=(float)0x3E2AAAAB
=(bin)0.00101010101010101010101011
=1/8+・・・+1/67108864
=11453246464/68719476736
=10/60+1/(67108864*3)≒10/60
0.017 =(float)0x3c888889
=(bin)0.00000100010001000100010001001
=1/64+・・・+1/536870912
=8947849/536870912
=1/60+7/(536870912*15)≒1/60
まあ実質1フレ単位ですがフレーム数とは非同期で計算はされていますね。
後日に続く
って感じに前後関係が追いにくいからblogって嫌いなのよね。このあたりはそのうちまとめて別ページにします。
まず判定差(ここではプレイの度に挙動が違う場合のある動作すべての意味)について、ガチ勢な方から提供頂いた貴重な情報をまとめてみます。
Ringedge時代はさらに他にも要因があったようですがとりあえずそこは省略します。
・筐体差
筐体(Nu/IOボード)に依存する固有の挙動。基本的に固定。アップデートで変化することがある。
・日付差/起動差
divaアプリ自体の再起動(筐体再起動/一旦Nuのサービスモードに戻る等)をする度に判定が変化することがある。
・ステージ差
特定のステージのみで判定が変化することがある。
・PV分岐差
分岐する/しないにより、その後のノーツの判定が変化することがある。
・時間差
上記の要因によらず、判定が変化することがある。
ということらしいですが、もちろん体感さっぱりわからん。
判別方法というのもあるらしく、
とのことだけど
「○が広ければxxx台」
とか言われてもどうやって○が広いかどうかを判別しろと。いや、原理は解るけどできません。
ところで、ここの記事はあくまで判定差の原因を突き止めようというだけで、ハイスコアを出してランキングインを目指そう、とかそういうページではないですよ。
腕があればお立ち台とか載ってみたいがな!
というわけなので、情報ソースはランカーの人達が気にするノーツ、つまりHOLDの入出ノーツになるけど、そんなに偶然キーとなるノーツばかりが変化する訳はないので、スコアタに関係ないノーツでもこのような事象は発生しているはず。
ただ、何をもって、「変化した」と定義するかは難しい。
たとえば「C-C MAX」が限られた条件だけで入るという判定差で、もしその筐体のすべての動作が正確に2倍速で動いたとして、超人が居ればやはり「C-C MAX」は入る。明らかに実時間で言えばCOOL期間は半分だけど、それは今回の検証として「変化した」とは言えない。
やはり、指標としては、ホールドノーツのちょうど5秒後にノーツがあって、MAXを取った後に判定がどうなるか、かな。
前回の解析結果によると、SAD/SAFEが一番期間が短いので、SAFEでホールド入って、5秒後のノーツでMAX取ったあとにSAFEを取れるか、とか。
でもHOLDを絡めないで検証したいんだよね。
※HOLDを絡めると、PVをそこまで進めないと検証できない、という、めんどくさいだけの話です。
まあそれはそれとして、課題だった奴。HOLD点の増加基準。結果解れば単純ですが、処理は結構やっかいでした。
はい、またいきなりソースです。HOLD関連処理関数です。
・引数
rcx=HOLD処理構造体アドレス
r8=押されているボタン(0x40)、○(0x80)、×(0x100)、□(0x200)のor
xmm1=前回この関数が呼ばれてからの経過時間
ちなみにこの関数自体は、どうやらVSYNCに同期して呼び出されるようです。
わりと冗長な処理とかもあるので関係ないところはがっつり削ったり順序変えたりしてます
14012C9F3: mov rdi,rcx
14012C9F6: mov ecx,dword ptr [rcx+0Ch] ;ホールド状態
14012CA15: dec ecx
14012CA17: je 000000014012CA97 ;ホールド中はjmp
14012CA1C: dec ecx
14012CA1E: je 000000014012CA73 ;MAX到達で飛ぶ
14012CA97: mov ecx,dword ptr [rdi+10h] ;ホールド中のボタン。
14012CA9A: test ecx,ecx
14012CA9C: je 000000014012CA44
14012CA9E: mov eax,ecx
14012CAA0: and eax,r8d
14012CAA3: cmp eax,ecx
14012CAA5: jne 000000014012CA84 ;押されているボタンが減った処理へ
14012CAAC: xorps xmm0,xmm0
14012CAA7: addss xmm6,dword ptr [rdi+14h] ;ホールド開始からの時間
14012CAB8: movss dword ptr [rdi+14h],xmm6 ;ホールド時間を更新
14012CAB4: mov r15d,dword ptr [rdi+18h] ;ホールド点(ゲーム中のHOLDボーナスバー表示)
14012CABD: subss xmm6,dword ptr [rdi+2Ch] ;最後にボタンが追加されてからの時間
14012CACC: comiss xmm6,dword ptr [140999A70h] ;5.000
14012CAD3: jb 000000014012CADD ;最後にボタン追加されてから5秒経ってないとjmp
14012CAD5: movss xmm6,dword ptr [140999A70h] ;5.000を超過したら5.000に丸め込み
14012CADD: comiss xmm6,dword ptr [rdi+1Ch] ;0.167。ただしボタン追加されたら0になる。
14012CAE1: jbe 000000014012CB2D ;ホールド開始から0.167s経過していないとjmp
14012CAE3: mov r8d,dword ptr [rdi+24h] ;1フレームあたりのホールド点。ボタン数で変化
14012CAE7: mov eax,r8d
14012CAEA: cdq
14012CAEB: sub eax,edx
14012CAED: sar eax,1
14012CAEF: movd xmm0,r8d
14012CAF4: cvtdq2ps xmm0,xmm0
14012CAF7: mulss xmm0,xmm6
14012CAFB: divss xmm0,dword ptr [rdi+20h] ;[rdi+20h]=常に0.017 xmm0=xmm0/0.017
14012CB00: cvttss2si ecx,xmm0
14012CB04: add eax,ecx
14012CB06: cdq
14012CB07: idiv eax,r8d
14012CB0A: mov ebx,eax
14012CB0C: imul ebx,r8d ;ebx=round([rdi+24h] * xmm6 / [rdi+20h])
14012CB10: cmp dword ptr [rdi],esi
14012CB12: jne 000000014012CB23
14012CB2D: mov ecx,dword ptr [rdi+30h] ;ホールド追加した時点の点数
14012CB30: add ecx,ebx
14012CB36: mov ebp,ecx
14012CB38: mov dword ptr [rdi+18h],ecx
;ebp=現時点の総ホールド点
;r15d=加算済みホールド点
14012CB41: sub ebp,r15d ;今回の加算点
14012CB52: comiss xmm6,dword ptr [140999A70h] ;5.000
14012CB59: mov dword ptr [rax+74h],3
14012CB60: mov dword ptr [rax+78h],ebx
14012CB63: mov dword ptr [rax+7Ch],r12d
14012CB67: jb 000000014012CA4C ;5.000未満
;MAX到達処理
14012CB6D: mov eax,dword ptr [rdi+34h] ;同時押しボタン数
14012CB7B: imul eax,eax,5DCh ;eax*1500=MAXボーナス
14012CB81: mov dword ptr [rdi+3Ch],eax ;MAX点を保持、この時点では加算されない
14012CB74: mov dword ptr [rdi+0Ch],2
14012CB84: jmp 000000014012CA4C
;ホールドMAXでここにくる
14012CA79: mov ebp,dword ptr [rdi+3Ch]
14012CA95: jmp 000000014012CA4C
14012CA4C:
14012CA60: mov eax,ebp ;戻り値代入
14012CA72: ret
つまりどういうことかというと、
・ホールドは開始から0.167秒は加算されない(知らなかった・・・)
・得点(MAX BONUS除く)はround(基準点(10~40) × ホールド秒 ÷ 0.017)
・ホールドMAX BONUSは、ホールドMAXの次のフレームで加算
ですね。
ところで、単精度浮動小数点の丸め込み誤差っていうのに気づいて、上記0.017とかは正確ではありません。
0.167=(float)0x3E2AAAAB
=(bin)0.00101010101010101010101011
=1/8+・・・+1/67108864
=11453246464/68719476736
=10/60+1/(67108864*3)≒10/60
0.017 =(float)0x3c888889
=(bin)0.00000100010001000100010001001
=1/64+・・・+1/536870912
=8947849/536870912
=1/60+7/(536870912*15)≒1/60
まあ実質1フレ単位ですがフレーム数とは非同期で計算はされていますね。
後日に続く
ビデオキャプチャの信頼性
2019.04.23
突然ですがビデオキャプチャの話題です。
なんかNTSC時代に似たような話題(http://d4.princess.ne.jp/multimedia/ntsc/)を掘り下げたことがありますが、今度はハイビジョン(HDMI)時代のお話です。
直球に言うと、「ゲームをキャプチャしたときに、それは100%正しく録画されているか」という話ですね。
結論から言うと、よほど気にしてキャプチャしない限りは、たいていの場合は「NO」となります。
さてそれではどういう現象が起きるかというと、
・フレームが欠落する
・フレームが増える(同じ画像が2フレーム記録される)
のどちらかとなります。場合によっては両方発生します。
■その1:ビデオキャプチャが59.94fpsと60.00fpsを正確に認識できない場合
そりゃあ辻褄あわせるのにどこかごまかさないとダメだよね。以上!
■その2:HDMI(映像+オーディオ)
とりあえず計算しやすくするために60.00fpsとします。数字が解りにくいだけで59.94fpsでも同じです。
ところでどうしてテレビは59.94fpsなんて中途半端な値なんだ、って思った人は、地上波アナログカラー放送が始まった頃の話をぐぐってください。どっかに書いてるかもしれません。
で、オーディオの方はとりあえず48KHzとしましょう。
つまりオーディオデータは1秒間に48000個あるわけですね。(ステレオだから96000個だろとかめんどくさいことは言わない。左右ペアのデータが48000個)
なので、60.00fpsだと、1フレームあたり48000÷60=800個のオーディオデータがあるはずです。
しかしこれが実際には、多少の誤差があります。なぜかというと、映像機器とオーディオ機器が別々の場合、それぞれの基準で時間を計るため、そこに誤差が出てきてしまうためです。PCやゲーム機から出力する場合、GPUとサウンドチップが別処理だったりするのでこうなりますね。
HDMIのデータとしては、1フレーム分の画像のあとに、「これがこのフレームと一緒になる音データ」というふうに、「約」800個のオーディオデータが送られてきます。なので、厳密に言うと、画像データとオーディオデータは同時には送信されていません。
さてこれを録画してデータ化するというのは、画像データとオーディオデータをひたすら溜めていくだけです。
するとどうでしょう。オーディオデータの個数が毎フレーム若干変動するので、いつのまにかどちらかが足りなくなってきます。
ここで、オーディオデータが足りなくなった場合、映像を1フレーム捨てることで辻褄を合わせます。
逆に、映像データが足りなくなった場合、同じ画像を2フレーム連続で保存することで辻褄を合わせます。
たとえばキャプチャソフトとして有名どころであるアマレコTVでは、その動作がヘルプに明確に記載されています。
アマレコTV ヘルプ
http://www.amarectv.com/amarectv4/manual/statusbar.html
4.録画情報
の (+) と (-)の説明です。
AVIで保存する場合、1フレーム毎にオーディオデータは何個という情報は持てないため、どうしてもこのような処理が必要になります。
また、mp4形式で直接録画する場合も、ps形式のmp4(AverMediaのほとんどの機種など大体はこの形式)であれば、同様になります。
ただし、ts形式のmp4であれば、1フレーム毎のオーディオデータの個数を保持できるため、このような調整はなく、確実に全フレーム・全オーディオデータを録画できます。
※厳密に言うとこれはps/tsの差分では無いのですが、事実上こうなっています。
■その3:HDMI(映像)+アナログオーディオ
結局のところ、その2と同じです。
アナログオーディオをA/Dコンバーターでデジタル化したあと、その2と同じように映像とオーディオを別々に溜めていきます。
すると、やはり同じ現象が発生するので、AVIもしくはps-mp4の場合、調整が必要になります。
・
・
・
・
・
というわけで、AverMediaの単体録画機や、アマレコTVなどのAVI系キャプチャでは、ほとんどの場合において、
フレーム欠落や追加などが起きていることになります。
つまり、世の中に大量にあるだろうそのような機材で録画された大半の動画はこういう観点では信用ならない、ということになります。
どこのノーツからどこのノーツまでが300フレームあるか、とかそういう確認には使えない、ということになりますね。
つまり新札猫にあったDIVAに繋がってたPLANTECの録画機はtsで撮れる貴重な録画機だったのだ・・・。
なので、2回同じPVを録画しても微妙にタイミングがずれている、というのはむしろこういう可能性の方が高いですね。
分配器で2分岐して同時にキャプチャ2台で録画しても、同じ物は撮れません。
という、筐体差を検証する上で、ネット上に転がっている動画は当てにならないかもしれない、というお話でした。
まあそれはそれとして、現役超ガチ勢(たぶん)の方から筐体差に関する貴重な情報を多々頂いた(しかもこの辺の話題で説明が付くような内容では無い)ので、それはそれで近いうちにまとめます。前回書いた内容を遙かに超えるレベルで筐体差は存在するようです。まあ自分で解らないからなぁ。
ゴールデンウィーク中になんか進展できるかな。。。用事あるから無理かな。。。
・メモ(というか課題)
ホールド点の増加基準
遅COOL/早COOLの判定基準
そもそもポーリングは一定間隔なのか
なんかNTSC時代に似たような話題(http://d4.princess.ne.jp/multimedia/ntsc/)を掘り下げたことがありますが、今度はハイビジョン(HDMI)時代のお話です。
直球に言うと、「ゲームをキャプチャしたときに、それは100%正しく録画されているか」という話ですね。
結論から言うと、よほど気にしてキャプチャしない限りは、たいていの場合は「NO」となります。
さてそれではどういう現象が起きるかというと、
・フレームが欠落する
・フレームが増える(同じ画像が2フレーム記録される)
のどちらかとなります。場合によっては両方発生します。
■その1:ビデオキャプチャが59.94fpsと60.00fpsを正確に認識できない場合
そりゃあ辻褄あわせるのにどこかごまかさないとダメだよね。以上!
■その2:HDMI(映像+オーディオ)
とりあえず計算しやすくするために60.00fpsとします。数字が解りにくいだけで59.94fpsでも同じです。
ところでどうしてテレビは59.94fpsなんて中途半端な値なんだ、って思った人は、地上波アナログカラー放送が始まった頃の話をぐぐってください。どっかに書いてるかもしれません。
で、オーディオの方はとりあえず48KHzとしましょう。
つまりオーディオデータは1秒間に48000個あるわけですね。(ステレオだから96000個だろとかめんどくさいことは言わない。左右ペアのデータが48000個)
なので、60.00fpsだと、1フレームあたり48000÷60=800個のオーディオデータがあるはずです。
しかしこれが実際には、多少の誤差があります。なぜかというと、映像機器とオーディオ機器が別々の場合、それぞれの基準で時間を計るため、そこに誤差が出てきてしまうためです。PCやゲーム機から出力する場合、GPUとサウンドチップが別処理だったりするのでこうなりますね。
HDMIのデータとしては、1フレーム分の画像のあとに、「これがこのフレームと一緒になる音データ」というふうに、「約」800個のオーディオデータが送られてきます。なので、厳密に言うと、画像データとオーディオデータは同時には送信されていません。
さてこれを録画してデータ化するというのは、画像データとオーディオデータをひたすら溜めていくだけです。
するとどうでしょう。オーディオデータの個数が毎フレーム若干変動するので、いつのまにかどちらかが足りなくなってきます。
ここで、オーディオデータが足りなくなった場合、映像を1フレーム捨てることで辻褄を合わせます。
逆に、映像データが足りなくなった場合、同じ画像を2フレーム連続で保存することで辻褄を合わせます。
たとえばキャプチャソフトとして有名どころであるアマレコTVでは、その動作がヘルプに明確に記載されています。
アマレコTV ヘルプ
http://www.amarectv.com/amarectv4/manual/statusbar.html
4.録画情報
の (+) と (-)の説明です。
AVIで保存する場合、1フレーム毎にオーディオデータは何個という情報は持てないため、どうしてもこのような処理が必要になります。
また、mp4形式で直接録画する場合も、ps形式のmp4(AverMediaのほとんどの機種など大体はこの形式)であれば、同様になります。
ただし、ts形式のmp4であれば、1フレーム毎のオーディオデータの個数を保持できるため、このような調整はなく、確実に全フレーム・全オーディオデータを録画できます。
※厳密に言うとこれはps/tsの差分では無いのですが、事実上こうなっています。
■その3:HDMI(映像)+アナログオーディオ
結局のところ、その2と同じです。
アナログオーディオをA/Dコンバーターでデジタル化したあと、その2と同じように映像とオーディオを別々に溜めていきます。
すると、やはり同じ現象が発生するので、AVIもしくはps-mp4の場合、調整が必要になります。
・
・
・
・
・
というわけで、AverMediaの単体録画機や、アマレコTVなどのAVI系キャプチャでは、ほとんどの場合において、
フレーム欠落や追加などが起きていることになります。
つまり、世の中に大量にあるだろうそのような機材で録画された大半の動画はこういう観点では信用ならない、ということになります。
どこのノーツからどこのノーツまでが300フレームあるか、とかそういう確認には使えない、ということになりますね。
つまり新札猫にあったDIVAに繋がってたPLANTECの録画機はtsで撮れる貴重な録画機だったのだ・・・。
なので、2回同じPVを録画しても微妙にタイミングがずれている、というのはむしろこういう可能性の方が高いですね。
分配器で2分岐して同時にキャプチャ2台で録画しても、同じ物は撮れません。
という、筐体差を検証する上で、ネット上に転がっている動画は当てにならないかもしれない、というお話でした。
まあそれはそれとして、現役超ガチ勢(たぶん)の方から筐体差に関する貴重な情報を多々頂いた(しかもこの辺の話題で説明が付くような内容では無い)ので、それはそれで近いうちにまとめます。前回書いた内容を遙かに超えるレベルで筐体差は存在するようです。まあ自分で解らないからなぁ。
ゴールデンウィーク中になんか進展できるかな。。。用事あるから無理かな。。。
・メモ(というか課題)
ホールド点の増加基準
遅COOL/早COOLの判定基準
そもそもポーリングは一定間隔なのか
 2019.06.01 22:36
|
2019.06.01 22:36
| 

